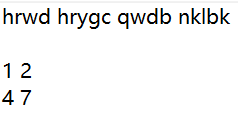关于希尔密码的简单研究

由于工作需要,接触了CTF的Crypto类型的题目,是一道关于希尔密码的题目,由于没有玩过这类题目,于是将过程记录下来做个笔记。
1. 希尔密码概要
简单的介绍下希尔密码。希尔密码属于古典密码,是运用矩阵原理的替换密码,发明者为 Lester S. Hill,发明时间是 1929 年。希尔密码在加解密过程中会大量使用到线性代数中的矩阵知识,所以对数学能力要求会高一点。下面是学习希尔密码的一些前提知识点:
矩阵:https://www.shuxuele.com/algebra/matrix-introduction.html
矩阵乘法:https://www.shuxuele.com/algebra/matrix-multiplying.html
矩阵的行列式:https://www.shuxuele.com/algebra/matrix-determinant.html
模逆元:https://en.wikipedia.org/wiki/Modular_multiplicative_inverse
上面这些参考链接,都可以看看,希尔密码的加解密都会涉及到这些。对于维基百科的东西,建议都看英文版,中文版写得太烂,完全不知道写的啥玩意儿。
2. 希尔密码的加密
先来学习希尔密码的加密步骤。
前提准备
在加密开始之前,首先得准备一些东西:
- 替换表:希尔密码属于替换密码,所以必须得先有一张替换表,这里设置的替换表如下
\[ \begin{array}{cc} a & b & c & d & e & f & g & h & i & j & k & l & m & n \\ 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \end{array} \]
\[ \begin{array}{cc} o & p & q & r & s & t & u & v & w & x & y & z \\ 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 \end{array} \]
密钥矩阵的维数:希尔密码的加解密都是依靠密钥矩阵的,规定密钥矩阵需为方块矩阵,也就是
n x n的矩阵,需第一时间确定n的值。这里设置密钥矩阵为 2 维矩阵,也就是2 x 2的矩阵明文信息:这里设置明文信息为
helloworld密钥信息:这里设置密钥为
hill在这里还有个步骤,就是需要校验密钥是否可逆,后面会专门讲这个点
矩阵转换
首先先将密钥信息转换为密钥矩阵。转换密钥矩阵时,需要根据最初设置的密钥矩阵维数来进行转换,将密钥以横向的方式依次变换成矩阵,如下:
\[ \begin{pmatrix} h & i \\ l & l \end{pmatrix} \]
在密钥转换成密钥矩阵时,需要注意两点:
- 密钥是横向填充到矩阵中的
- 如果密钥的长度不够填充密钥矩阵时,需用替换表中的字母依次填充。如果密钥的长度超出矩阵数量时,则只取相应长度的密钥填充即可
举例:
密钥矩阵的维度设置为
2,密钥为ice,替换表还是上面那个。因为密钥长度不够填充矩阵,需要用替换表中的字符来补足,如下: \[ \begin{pmatrix} i & c \\ e & a \end{pmatrix} \] 密钥矩阵的维度设置为2,密钥为green,替换表还是上面那个。因为密钥长度超出了矩阵数量,所以只截取相应的长度,如下: \[ \begin{pmatrix} g & r \\ e & e \end{pmatrix} \]
得到转换后的密钥矩阵之后,需要将其按照替换表替换为数字型的密钥矩阵,如下:
\[ \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \]
得到密钥矩阵之后,现在来进行明文的矩阵转换。明文的矩阵,行数需和密钥矩阵维度相同,并且是以纵向的方式进行矩阵填充的,如下:
\[ \begin{pmatrix} h & l & o & o & l \\ e & l & w & r & d \end{pmatrix} \]
在明文转换成矩阵时,需要注意两点:
- 明文是纵向填充到矩阵中的
- 如果明文的长度不够填充矩阵时,需要用
x补足举例:
密钥矩阵的维度设置为
2,明文为hello,替换表还是上面那个。因为明文长度不够填充矩阵,需要用x来补足,如下: \[ \begin{pmatrix} h & l & o \\ e & l & x \end{pmatrix} \]
将明文矩阵转换为数字型的明文矩阵,如下:
\[ \begin{pmatrix} 7 & 11 & 14 & 14 & 11 \\ 4 & 11 & 22 & 17 & 3 \end{pmatrix} \]
由此,两个需要的矩阵都有了之后,现在可以正式开始进行加密了。
正式加密
希尔密码加密,需要用密钥矩阵与明文矩阵的每一个列向量(column vector)相乘,所以先将明文矩阵分割成列向量的形式,如下:
\[ \begin{pmatrix} 7 \\ 4 \end{pmatrix} \begin{pmatrix} 11 \\ 11 \end{pmatrix} \begin{pmatrix} 14 \\ 22 \end{pmatrix} \begin{pmatrix} 14 \\ 17 \end{pmatrix} \begin{pmatrix} 11 \\ 3 \end{pmatrix} \]
然后将密钥矩阵和每一个列向量相乘,如与第一个列向量相乘,就像这样:
\[ \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 7 \\ 4 \end{pmatrix} \]
而相乘的方式就是矩阵的乘法方式,2 x 2的矩阵乘法如下:
\[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax & + & by \\ cx & + & dy \end{pmatrix} \]
转换为密钥和列向量的话,就像下面这样:
\[ \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 7 \\ 4 \end{pmatrix} = \begin{pmatrix} 7\times7 & + & 8\times4 \\ 11\times7 & + & 11\times4 \end{pmatrix} = \begin{pmatrix} 81 \\ 121 \end{pmatrix} \]
得到相乘后的结果之后,再将其与 26 相模,如下:
\[ \begin{pmatrix} 81 \\ 121 \end{pmatrix} \equiv \begin{pmatrix} 3 \\ 17 \end{pmatrix} \mod 26 \]
最后将数字转换成替换表中的字符即可,如下: \[ \begin{pmatrix} 3 \\ 17 \end{pmatrix} = \begin{pmatrix} d \\ r \end{pmatrix} \]
最终结果
根据上面的加密步骤,计算出所有的密文,如下:
\[ \begin{pmatrix} h & i \\ l & l \end{pmatrix} \begin{pmatrix} h \\ e \end{pmatrix} \equiv \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 7 \\ 4 \end{pmatrix} \equiv \begin{pmatrix} 7\times7 & + & 8\times4 \\ 11\times7 & + & 11\times4 \end{pmatrix} \equiv \begin{pmatrix} 81 \\ 121 \end{pmatrix} \equiv \begin{pmatrix} 3 \\ 17 \end{pmatrix} \mod 26 = \begin{pmatrix} d \\ r \end{pmatrix} \]
\[ \begin{pmatrix} h & i \\ l & l \end{pmatrix} \begin{pmatrix} l \\ l \end{pmatrix} \equiv \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 11 \\ 11 \end{pmatrix} \equiv \begin{pmatrix} 7\times11 & + & 8\times11 \\ 11\times11 & + & 11\times11 \end{pmatrix} \equiv \begin{pmatrix} 165 \\ 242 \end{pmatrix} \equiv \begin{pmatrix} 9 \\ 8 \end{pmatrix} \mod 26 = \begin{pmatrix} j \\ i \end{pmatrix} \]
\[ \begin{pmatrix} h & i \\ l & l \end{pmatrix} \begin{pmatrix} o \\ w \end{pmatrix} \equiv \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 14 \\ 22 \end{pmatrix} \equiv \begin{pmatrix} 7\times14 & + & 8\times22 \\ 11\times14 & + & 11\times22 \end{pmatrix} \equiv \begin{pmatrix} 274 \\ 396 \end{pmatrix} \equiv \begin{pmatrix} 14 \\ 6 \end{pmatrix} \mod 26 = \begin{pmatrix} o \\ g \end{pmatrix} \]
\[ \begin{pmatrix} h & i \\ l & l \end{pmatrix} \begin{pmatrix} o \\ r \end{pmatrix} \equiv \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 14 \\ 17 \end{pmatrix} \equiv \begin{pmatrix} 7\times14 & + & 8\times17 \\ 11\times14 & + & 11\times17 \end{pmatrix} \equiv \begin{pmatrix} 234 \\ 341 \end{pmatrix} \equiv \begin{pmatrix} 0 \\ 3 \end{pmatrix} \mod 26 = \begin{pmatrix} a \\ d \end{pmatrix} \]
\[ \begin{pmatrix} h & i \\ l & l \end{pmatrix} \begin{pmatrix} l \\ d \end{pmatrix} \equiv \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} \begin{pmatrix} 11 \\ 3 \end{pmatrix} \equiv \begin{pmatrix} 7\times11 & + & 8\times3 \\ 11\times11 & + & 11\times3 \end{pmatrix} \equiv \begin{pmatrix} 101 \\ 154 \end{pmatrix} \equiv \begin{pmatrix} 23 \\ 24 \end{pmatrix} \mod 26 = \begin{pmatrix} x \\ y \end{pmatrix} \]
最后,明文为helloworld,密钥为hill的情况下,希尔密码加密后得到的密文为drjiogadxy。
3. 希尔密码的解密
现在来学习希尔密码的解密步骤,相对于加密来说,希尔密码的解密会稍微难一些。
前提准备
和加密一样,在解密之前,需要准备一些东西,与加密准备的东西差不多,如下:
- 替换表:同加密一样,解密同样需要一张替换表,并且需要和加密时的一致,如下
\[ \begin{array}{cc} a & b & c & d & e & f & g & h & i & j & k & l & m & n \\ 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \end{array} \]
\[ \begin{array}{cc} o & p & q & r & s & t & u & v & w & x & y & z \\ 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 \end{array} \]
密钥矩阵的维数:需与加密时的一致,设置密钥矩阵为 2 维矩阵,也就是
2 x 2的矩阵密文信息:注意这里设置的是密文信息,也就是刚才加密得到的
drjiogadxy密钥信息:需与加密时的一致,设置密钥为
hill
密文矩阵转换
这里先将密文转换成矩阵,并且分割成列向量的形式,如下:
\[ \begin{pmatrix} d & j & o & a & x \\ r & i & g & d & y \end{pmatrix} = \begin{pmatrix} 3 & 9 & 14 & 0 & 23 \\ 17 & 8 & 6 & 3 & 24 \end{pmatrix} = \begin{pmatrix} 3 \\ 17 \end{pmatrix} \begin{pmatrix} 9 \\ 8 \end{pmatrix} \begin{pmatrix} 14 \\ 6 \end{pmatrix} \begin{pmatrix} 0 \\ 3 \end{pmatrix} \begin{pmatrix} 23 \\ 24 \end{pmatrix} \]
求取逆矩阵
在解密过程中,最重要的一步就是求密钥矩阵的逆矩阵,求得了逆矩阵之后,其余步骤就和加密步骤没什么区别了。需要注意的是,这里指的逆矩阵不是一般的逆矩阵,与平时提到的逆矩阵大不相同,计算方式也完全不一样。
一般逆矩阵的计算公式如下: \[ A^{-1} = { \frac {A^{*}}{|A|} } = { \frac 1{|A|} } \times A^{*} \] 其中 $ A $ 为矩阵,$ A^{-1} $ 为 $ A $ 的逆矩阵,$ A^{*} $ 为 $ A $ 的伴随矩阵,$ {|A|} $ 为 $ A $ 的行列式。
而希尔密码密钥矩阵的逆矩阵计算公式如下: \[ K^{-1} = d^{-1} \times adj(K) \] 其中 $ K $ 为密钥矩阵,$ K^{-1} $ 为 $ K $ 的逆矩阵,$ d $ 为 $ K $ 的行列式,$ adj(K) $ 为 $ K $ 的伴随矩阵。
从上面的两个公式来看,两个都是用矩阵行列式的倒数去乘以矩阵的伴随矩阵,从而得到矩阵的逆。看上去似乎两个没什么区别,实际上,希尔密码的矩阵求逆,还需要与替换表的长度,也就是 26,进行相关的模运算,这就是两者的区别,下面会详细讲解希尔密码矩阵的求逆步骤。
这里有个很大的误区,网上找了很多篇帖子,发现大家求的都是一般的逆矩阵,包括各种CTF题也是按照一般的逆矩阵来加密或解密,不知道是出题人对希尔密码理解有误,还是说希尔密码有另一种计算方式,反正看到的 CTF 题,都不是维基百科的那种计算方式。
网上搜到的关于希尔密码的资料,也的确写的是逆矩阵这三个字,导致很容易就理解为一般的逆矩阵,也不知道为什么没有重新取一个名字,这里困惑了好久。
上面讲了一大堆理论知识,现在开始来进行密钥矩阵求逆的步骤。
Step 1
首先,需要求取密钥矩阵行列式的乘法逆。
2 x 2矩阵的行列式计算方式如下:
\[ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \times d - b \times c \]
带入密钥矩阵,结果如下:
\[ \begin{vmatrix} h & i \\ l & l \end{vmatrix} = \begin{vmatrix} 7 & 8 \\ 11 & 11 \end{vmatrix} = 7 \times 11 - 8 \times 11= -11 \]
将行列式的结果模 26:
\[ -11 \equiv 15 \mod {26} \]
再求取其的乘法逆,乘法逆求取方式如下:
\[ d \times d^{-1} \equiv 1 \mod 26 \]
带入相应的数字,如下:
\[ 15 \times x \equiv 1 \mod 26 \]
求乘法逆可以通过枚举的方式,下面是Python代码:
| |
最后得到结果为7,如下:
\[ 15 \times 7 \equiv 105 \equiv 1 \mod 26 \]
Step 2
接着求取密钥矩阵的伴随矩阵。
2 x 2矩阵的伴随矩阵如下计算:
\[ adj \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \]
带入密钥矩阵的话,结果如下:
\[ adj \begin{pmatrix} h & i \\ l & l \end{pmatrix} = adj \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} = \begin{pmatrix} 11 & -8 \\ -11 & 7 \end{pmatrix} \]
得到结果之后,需要在负值上加上 26,以得到 0 ~ 25 之间的数字,如下:
\[ \begin{pmatrix} 11 & -8 \\ -11 & 7 \end{pmatrix} = \begin{pmatrix} 11 & -8 + 26 \\ -11 + 26 & 7 \end{pmatrix} \]
最后得到结果,如下:
\[ \begin{pmatrix} 11 & 18 \\ 15 & 7 \end{pmatrix} \]
Step 3
最后来求密钥矩阵的逆。
得到行列式的乘法逆和伴随矩阵之后,将两者相乘的结果,再模上 26,就得到了逆矩阵,如下:
\[ 7 \times \begin{pmatrix} 11 & 18 \\ 15 & 7 \end{pmatrix} \equiv \begin{pmatrix} 7 \times 11 & 7 \times 18 \\ 7 \times 15 & 7 \times 7 \end{pmatrix} \equiv \begin{pmatrix} 77 & 126 \\ 105 & 49 \end{pmatrix} \equiv \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} \mod 26 \]
解密
得到了逆矩阵之后,与加密步骤一样,用逆矩阵乘以密文矩阵的每一项列向量,再与 26 相模,即可得到相应的明文,如下:
\[ \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} \begin{pmatrix} 3 \\ 17 \end{pmatrix} \equiv \begin{pmatrix} 25 \times 3 & + & 22 \times 17 \\ 1 \times 3 & + & 23 \times 17 \end{pmatrix} \equiv \begin{pmatrix} 449 \\ 394 \end{pmatrix} \equiv \begin{pmatrix} 7 \\ 4 \end{pmatrix} \mod 26 = \begin{pmatrix} h \\ e \end{pmatrix} \]
\[ \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} \begin{pmatrix} 9 \\ 8 \end{pmatrix} \equiv \begin{pmatrix} 25 \times 9 & + & 22 \times 8 \\ 1 \times 9 & + & 23 \times 8 \end{pmatrix} \equiv \begin{pmatrix} 401 \\ 193 \end{pmatrix} \equiv \begin{pmatrix} 11 \\ 11 \end{pmatrix} \mod 26 = \begin{pmatrix} l \\ l \end{pmatrix} \]
\[ \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} \begin{pmatrix} 14 \\ 6 \end{pmatrix} \equiv \begin{pmatrix} 25 \times 14 & + & 22 \times 6 \\ 1 \times 14 & + & 23 \times 6 \end{pmatrix} \equiv \begin{pmatrix} 482 \\ 152 \end{pmatrix} \equiv \begin{pmatrix} 14 \\ 22 \end{pmatrix} \mod 26 = \begin{pmatrix} o \\ w \end{pmatrix} \]
\[ \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} \begin{pmatrix} 0 \\ 3 \end{pmatrix} \equiv \begin{pmatrix} 25 \times 0 & + & 22 \times 3 \\ 1 \times 0 & + & 23 \times 3 \end{pmatrix} \equiv \begin{pmatrix} 66 \\ 69 \end{pmatrix} \equiv \begin{pmatrix} 14 \\ 17 \end{pmatrix} \mod 26 = \begin{pmatrix} o \\ r \end{pmatrix} \]
\[ \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} \begin{pmatrix} 23 \\ 24 \end{pmatrix} \equiv \begin{pmatrix} 25 \times 23 & + & 22 \times 24 \\ 1 \times 23 & + & 23 \times 24 \end{pmatrix} \equiv \begin{pmatrix} 1103 \\ 575 \end{pmatrix} \equiv \begin{pmatrix} 11 \\ 3 \end{pmatrix} \mod 26 = \begin{pmatrix} l \\ d \end{pmatrix} \]
最后,密文为drjiogadxy,密钥为hill的情况下,希尔密码解密后得到的明文为helloworld。
4. CTF 实战
这是XMan选拔赛的一道题,很简单,题目就一个TXT文本,打开一看,里面有一串字符串和一个矩阵,如下:
一看就知道是关于希尔密码的题,字符串为密文,矩阵为密钥。先求密钥矩阵的逆:
\[ 行列式:\\ \begin{vmatrix} 1 & 2 \\ 4 & 7 \end{vmatrix} \equiv 1 \times 7 - 2 \times 4 \equiv -1 \equiv 25 \mod 26 \]
\[ 行列式的乘法逆:\\ 25 \times x \equiv 1 \mod 26 \\ = \\ 25 \times 25 \equiv 1 \mod 26 \]
\[ 伴随矩阵:\\ adj \begin{pmatrix} 1 & 2 \\ 4 & 7 \end{pmatrix} = \begin{pmatrix} 7 & -2 \\ -4 & 1 \end{pmatrix} = \begin{pmatrix} 7 & -2 + 26 \\ -4 + 26 & 1 \end{pmatrix} = \begin{pmatrix} 7 & 24 \\ 22 & 1 \end{pmatrix} \]
\[ 逆矩阵:\\ 25 \times \begin{pmatrix} 7 & 24 \\ 22 & 1 \end{pmatrix} \equiv \begin{pmatrix} 25 \times 7 & 25 \times 24 \\ 25 \times 22 & 25 \times 1 \end{pmatrix} \equiv \begin{pmatrix} 175 & 600 \\ 550 & 25 \end{pmatrix} \equiv \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \mod 26 \]
求得逆矩阵之后,再把密文转换为矩阵并分割成列向量的形式,如下:
\[ \begin{pmatrix} h & w & h & y & c & w & b & k & b \\ r & d & r & g & q & d & n & l & k \end{pmatrix} = \begin{pmatrix} 7 & 22 & 7 & 24 & 2 & 22 & 1 & 10 & 1 \\ 17 & 3 & 17 & 6 & 16 & 3 & 13 & 11 & 10 \end{pmatrix} \\ = \\ \begin{pmatrix} 7 \\ 17 \end{pmatrix} \begin{pmatrix} 22 \\ 3 \end{pmatrix} \begin{pmatrix} 7 \\ 17 \end{pmatrix} \begin{pmatrix} 24 \\ 6 \end{pmatrix} \begin{pmatrix} 2 \\ 16 \end{pmatrix} \begin{pmatrix} 22 \\ 3 \end{pmatrix} \begin{pmatrix} 1 \\ 13 \end{pmatrix} \begin{pmatrix} 10 \\ 11 \end{pmatrix} \begin{pmatrix} 1 \\ 10 \end{pmatrix} \]
开始解密,用逆矩阵乘以密文矩阵的每一个列向量并与 26 相模,得到明文,如下:
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 7 \\ 17 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 7 & + & 2 \times 17 \\ 4 \times 7 & + & 25 \times 17 \end{pmatrix} \equiv \begin{pmatrix} 167 \\ 453 \end{pmatrix} \equiv \begin{pmatrix} 11 \\ 11 \end{pmatrix} \mod 26 = \begin{pmatrix} l \\ l \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 22 \\ 3 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 22 & + & 2 \times 3 \\ 4 \times 22 & + & 25 \times 3 \end{pmatrix} \equiv \begin{pmatrix} 424 \\ 163 \end{pmatrix} \equiv \begin{pmatrix} 8 \\ 7 \end{pmatrix} \mod 26 = \begin{pmatrix} i \\ h \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 7 \\ 17 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 7 & + & 2 \times 17 \\ 4 \times 7 & + & 25 \times 17 \end{pmatrix} \equiv \begin{pmatrix} 167 \\ 453 \end{pmatrix} \equiv \begin{pmatrix} 11 \\ 11 \end{pmatrix} \mod 26 = \begin{pmatrix} l \\ l \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 24 \\ 6 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 24 & + & 2 \times 6 \\ 4 \times 24 & + & 25 \times 6 \end{pmatrix} \equiv \begin{pmatrix} 468 \\ 246 \end{pmatrix} \equiv \begin{pmatrix} 0 \\ 12 \end{pmatrix} \mod 26 = \begin{pmatrix} a \\ m \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 2 \\ 16 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 2 & + & 2 \times 16 \\ 4 \times 2 & + & 25 \times 16 \end{pmatrix} \equiv \begin{pmatrix} 70 \\ 408 \end{pmatrix} \equiv \begin{pmatrix} 18 \\ 18 \end{pmatrix} \mod 26 = \begin{pmatrix} s \\ s \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 22 \\ 3 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 22 & + & 2 \times 3 \\ 4 \times 22 & + & 25 \times 3 \end{pmatrix} \equiv \begin{pmatrix} 424 \\ 163 \end{pmatrix} \equiv \begin{pmatrix} 8 \\ 7 \end{pmatrix} \mod 26 = \begin{pmatrix} i \\ h \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 1 \\ 13 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 1 & + & 2 \times 13 \\ 4 \times 1 & + & 25 \times 13 \end{pmatrix} \equiv \begin{pmatrix} 45 \\ 329 \end{pmatrix} \equiv \begin{pmatrix} 19 \\ 17 \end{pmatrix} \mod 26 = \begin{pmatrix} t \\ r \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 10 \\ 11 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 10 & + & 2 \times 11 \\ 4 \times 10 & + & 25 \times 11 \end{pmatrix} \equiv \begin{pmatrix} 212 \\ 315 \end{pmatrix} \equiv \begin{pmatrix} 4 \\ 3 \end{pmatrix} \mod 26 = \begin{pmatrix} e \\ d \end{pmatrix} \]
\[ \begin{pmatrix} 19 & 2 \\ 4 & 25 \end{pmatrix} \begin{pmatrix} 1 \\ 10 \end{pmatrix} \equiv \begin{pmatrix} 19 \times 1 & + & 2 \times 10 \\ 4 \times 1 & + & 25 \times 10 \end{pmatrix} \equiv \begin{pmatrix} 39 \\ 254 \end{pmatrix} \equiv \begin{pmatrix} 13 \\ 20 \end{pmatrix} \mod 26 = \begin{pmatrix} n \\ u \end{pmatrix} \]
最后得出结果:密文为hrwdhrygcqwdbnklbk,密钥为bceh,解密的明文为llihllamssihtrednu。
由于题目是网上薅的,题目没给完整,题目描述里面有 “爬下山坡” 的提示,再结合解出来的明文一观察,实际上是要对明文进行反向处理,最后得出正确得 flag 为:XMAN{under this small hill}
5. 其他问题
- 密钥需设置为可逆的
矩阵有不可逆矩阵。作为密钥矩阵,如果不可逆的话,那么将无法进行解密。所以在定义密钥之前,需要判断该密钥是否可逆,一般的方法是利用密钥矩阵的行列式,当行列式不为 0,并且与替换表长度互质的情况下,该密钥才可用来解密。拿上面的hill举例,如下:
\[ \begin{vmatrix} h & i \\ l & l \end{vmatrix} \equiv \begin{vmatrix} 7 & 8 \\ 11 & 11 \end{vmatrix} \equiv 7 \times 11 - 8 \times 11 \equiv -11 \equiv 15 \mod 26 \]
求得的结果为 15,15 满足不为 0 的要求,并且也与 26 互质,所以该密钥可以用来解密。
如果设置密钥为不可逆的密钥,会发生什么情况呢?例如设置密钥为fcdj,转换为矩阵为:
\[ \begin{pmatrix} 5 & 2 \\ 3 & 9 \end{pmatrix} \]
它的行列式如下:
\[ \begin{vmatrix} 5 & 2 \\ 3 & 9 \end{vmatrix} \equiv 5 \times 9 - 2 \times 3 \equiv 39 \equiv 13 \mod 26 \]
得到行列式为 13,而 13 与 26 并不互质,因为他们存在两个公约数:1、13
用该矩阵来加密没任何问题,问题会出现在解密上。在解密的时候,用该矩阵求逆矩阵时,在求行列式的乘法逆的地方就会卡住,是找不到相应的乘法逆的,如果不相信的话,可以用脚本跑一跑。
找不到乘法逆,也就找不到解密用的逆矩阵,也就解不了密。所以在设置密钥的时候,一定要先用上面的公式来确认密钥是否为可逆的。
- 替换表与 26
关于替换表与 26 这个数字,得提一提。
替换表不一定得是按照顺序排列的 26 个字母,也可以打乱顺序排列,甚至可以不用字母,用中文当替换表也是可以的,只是相应的计算都得根据替换表发生变化而已。例如替换表换成下面这样,一样可以进行加解密:
\[ \begin{array}{cc} h & e & l & l & o & w & o & r & l & d \\ 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \end{array} \]
而 26 这个数字,在文中使用 26 来与其他表达式进行计算,是因为替换表刚好有 26 个字符。这个 26 是根据替换表的长度来的,例如上面的替换表,如果要进行相应的计算,那应该将 26 换成 10 才对。
- 明文与密钥的填充事项
在前面我们提到了关于明文的长度不够填充矩阵和密钥的长度大于或小于矩阵的填充长度的相关问题,这个问题网上搜索了很多资料,没有统一的答案。有的说将 0 作为填充物,有的说将 E 作为填充物,说啥的都有。
在这里我觉得,填充什么都没有关系,这个可以自定义的,但是加解密时必须一致,例如加密时填充的是 x,那么解密时也应该填充 x,所以这个地方只需要加解密保持一致,填充什么字符都无所谓。
- 网上的希尔密码资料
网上看了很多关于希尔密码的资料,水平参差不齐,特别是前面提到的关于解密时的逆矩阵计算方法,各种各样的解法都有。国内的资料,说实话水平的确要差些,对比一下中英文的希尔密码的维基百科,那简直一个天上一个地下。所以如果需要深入学习希尔密码的相关知识,建议搜索英文版的资料进行学习。
- 逆矩阵相关问题
对于解密时的逆矩阵,研究了一下,发现当密钥矩阵的一般逆矩阵,也就是用 $ A^{-1} = { \frac {A^{*}}{|A|} } = { \frac 1{|A|} } \times A^{*} $ 公式求出来的逆矩阵,它的每一个值都为整数时,该密钥矩阵就可以用一般逆矩阵的方式来解密密文,比如上面的 CTF 例子,它的一般逆矩阵是这样的:
\[ \begin{pmatrix} 1 & 2 \\ 4 & 7 \end{pmatrix} ^{-1} = \begin{pmatrix} -7 & 2 \\ 4 & -1 \end{pmatrix} \]
用这个逆矩阵对密文矩阵的每一个列向量进行相乘并取模 26,可以发现也能求出明文,下面是一个列向量的例子:
\[ \begin{pmatrix} -7 & 2 \\ 4 & -1 \end{pmatrix} \begin{pmatrix} 7 \\ 17 \end{pmatrix} \equiv \begin{pmatrix} -7 \times 7 & + & 2 \times 17 \\ 4 \times 7 & + & -1 \times 17 \\ \end{pmatrix} \equiv \begin{pmatrix} -15 \\ 11 \end{pmatrix} \equiv \begin{pmatrix} 11 \\ 11 \end{pmatrix} \mod 26 = \begin{pmatrix} l \\ l \end{pmatrix} \]
通过这种方式解出来的答案和之前用的方式解出来的答案是一模一样的。当然,如果你觉得这是巧合的话,可以设置密钥为bcab,转换成矩阵就为:
\[ \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} \]
而对应的逆矩阵为:
\[ \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} ^{-1} = \begin{pmatrix} 1 & -2 \\ 0 & 1 \end{pmatrix} \]
可以看到逆矩阵中的值都为整数,用该密钥来进行加密,也是可以解密出来的,并且用两种方式解出来的答案是一致的。
对于这个为什么会这样,实在是没找到答案,加上自己的数学功底不好,想不明白这问题。但是,需要提的一点就是,许多 CTF 题都是考的这样的希尔密码加解密,很容易就让大家误以为希尔密码就该这样解,我觉得这点不太好。
我还是觉得第一种方式的加解密是最规范的,这一种感觉像是走后门似的,主要吧,这后门还时通时不通,万一要是遇到逆矩阵中的值存在分数的呢,这个方式就完全解不了。
6. END
这篇文章终于写完了,零零散散的写了将近半个月,可算是把它给写完了。其实理解透了这个密码算法原理就没那么难写了,之前因为一些垃圾文章,导致一直没彻底理解到该密码算法的原理,弄得一直写写删删的。所以学这种东西还得看国外的文章,即使看不懂英文,用 Google 翻译机翻都比国内的大多数文章写的好。当然这篇文章写得可能也有一些错误,如果各位大大发现哪有不正确的,望不吝赐教。
讲解最完整的希尔密码理论:https://crypto.interactive-maths.com/hill-cipher.html
矩阵计算器:
https://matrix.reshish.com/zh/inverse.php
https://www.shuxuele.com/algebra/matrix-calculator.html
https://zs.symbolab.com/solver/matrix-multiply-calculator
希尔密码在线工具:
https://www.tooleyes.com/app/hill_cipher.html
http://www.atoolbox.net/Tool.php?Id=914
公倍数,公约数在线计算器: https://www.osgeo.cn/app/s1770
文中 CTF 题目文件:CRYPTO-HILL.zip